Olika tal - Övning
|
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||
Tiosystemet
151.
Välj den expanderade formen för det antal.
| en. |
500 + 5 + 50
|
||
| b. |
500 + 50 + 5
|
||
| c.. |
5 + 50 + 500
|
||
| d. |
50 + 500 + 5
|
152.
Välj numret för utökad notation.
| en. |
999
|
||
| b. |
990
|
||
| c.. |
99
|
||
| d. |
909
|
Rätt svar
Uppgift 2 c)
Rätt svar: 0,008
Uppgift 2 d)
Rätt svar: 0,075
Uppgift 2 e)
Rätt svar: 0,2765
Uppgift 2 f)
Rätt svar: 0,00002
Uppgift 2 g)
Rätt svar: 3,5
Rätt svar
Lösningar [stäng]
Uppgift 3 a)
Rätt svar: 7,5
Uppgift 3 b)
Rätt svar: 5,89
Uppgift 3 c)
Rätt svar: 3,008
Uppgift 3 d)
Rätt svar: 19,2
Uppgift 3 e)
Rätt svar: 2,0083
Uppgift 3 f)
Rätt svar: 5,062
Uppgift 3 g)
Rätt svar: 35
Uppgift 3 a)
Rätt svar: 7,5
Uppgift 3 b)
Rätt svar: 5,89
Uppgift 3 c)
Rätt svar: 3,008
Uppgift 3 d)
Rätt svar: 19,2
Uppgift 3 e)
Rätt svar: 2,0083
Uppgift 3 f)
Rätt svar: 5,062
Uppgift 3 g)
Rätt svar: 35
Decimaltal
Om vi tittar på tallinjen så ser vi att det finns mellanrum mellan de naturliga talen. Om vi markerar ett tal som ligger någonstans mellan två naturliga tal på tallinjen, så kan det talet inte vara ett heltal. Däremot kan det vara ettdecimaltal.
Om vi till exempel markerar ett tal som ligger mittemellan de naturliga talen 1 och 2 på tallinjen, så är detta tal det decimala talet 1,5.
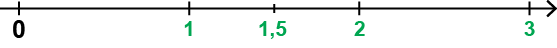
Ett decimaltal är med hjälp av ett decimaltecken uppdelat i en heltalsdel och en decimaldel. Heltalsdelen står till vänster om decimaltecknet och decimaldelen står till höger om decimaltecknet. I decimaltalet 1,5 är därför siffran 1 talets heltalsdel och siffran 5 är talets decimaldel.
Även i decimaltal har siffrorna som talet består av olika stort värde beroende på deras position i talet. För decimaltalets heltalsdel fungerar siffrornas position på samma sätt som för naturliga tal. Siffrorna som hör till decimaldelen anger tiondelar, hundradelar, tusendelar, och så vidare.
På samma sätt som med naturliga tal kan vi skriva ett decimaltal i utvecklad form som en summa av termer.
Decimaltalet 37,92 skrivas som summan av siffrornas värde så här
30+7+0,9+0,02=37,92
Hur mycket är siffran 4 värd i följande tal?
- 12,94
- 0,49
- 546,1
Lösningsförslag:
- Siffran 4 i talet 12,94 anger antalet hundradelar. Därför har siffran 4 i talet värdet 0,04, vilket är samma sak som 4 hundradelar.
- Siffran 4 i talet 0,49 anger antalet tiondelar. Därför har siffran 4 i talet 0,49 värdet 0,4, vilket är samma sak som 4 tiondelar.
- Siffran 4 i talet 546,1 anger antalet tiotal. Därför har siffran 4 i talet 546,1 värdet 40.
Skriv följande tal i utvecklad form
- 12,94
- 0,49
- 546,1
Lösningsförslag:
- Talet 12,94 består av siffrorna 1, 2, 9 och 4. Tiotalssiffran 1 har värdet 10, entalssiffran 2 har värdet 2, tiondelssiffran 9 har värdet 0,9 (alltså 9 tiondelar) och hundradelssiffran 4 har värdet 0,04 (alltså 4 hundradelar).
Talet 12,94 skrivet i utvecklad form blir därför
10+2+0,9+0,04 -
Talet 0,49 består av siffrorna 0, 4 och 9. Entalssiffran 0 har värdet 0, tiondelssiffran 4 har värdet 0,4 (alltså 4 tiondelar) och hundradelssiffran 9 har värdet 0,09 (alltså 9 hundradelar).
Eftersom entalssiffran är 0 behöver vi inte ta med entalet när vi skrivet talet 0,49 i utvecklad form. Talet 0,49 skrivet i utvecklad form blir därför
0,4+0,09 -
Talet 546,1 består av siffrorna 5, 4, 6 och 1. Hundratalssiffran 5 har värdet 500, tiotalssiffran 4 har värdet 40, entalssiffran 6 har värdet 6 och tiondelssiffran 1 har värdet 0,1 (alltså 1 tiondel).
Talet 546,1 skrivet i utvecklad form blir därför
500+40+6+0,1
Naturliga tal
När vi vill skriva hur många eller hur mycket det finns av något, så använder vi tal som består av siffrorna 0, 1, 2, 3, 4, 5, 6, 7, 8 och 9. Var för sig eller tillsammans kan dessa tio siffror bilda olika tal, som kan vara hur stora som helst. Dessa tal kallar vi de naturliga talen. Alla naturliga tal är heltal.
Vi kan markera naturliga tal på tallinjen.
Om vi har två olika naturliga tal, till exempel 13 och 31, så betyder siffrorna 1 och 3 olika saker beroende på deras position i talet. I talet 13 betyder ju siffran 3 att talet innehåller 3 ental (3), medan siffran 3 i talet 31 betyder att talet innehåller 3 tiotal (30).
En siffra i ett naturligt tal har alltså olika stort värde beroende på siffrans position i talet. Vi kan skriva talets värde som summan av siffrornas värde i talet.
Heltalet 3792 skrivas som summan av siffrornas värde så här
3000+700+90+2=3792
Är ett tal skrivet på detta sätt som en summa av siffrornas värde säger vi att talet är skrivet i utvecklad form. Ibland kan det vara lättare att räkna med tal om vi skriver om talen i utvecklad form.
Hur mycket är siffran 7 värd i följande tal?
- 72
- 137
- 720
- Siffran 7 i talet 72 anger antalet tiotal. Därför anger tiotalssiffran 7 värdet 70.
- Siffran 7 i talet 137 anger antalet ental. Därför anger entalssiffran 7 värdet 7.
- Siffran 7 i talet 720 anger antalet hundratal. Därför anger hundratalssiffran 7 värdet 700.
Skriv följande tal i utvecklad form
- 72
- 137
- 720
Lösningsförslag:
- Talet 72 består av siffrorna 7 och 2, där tiotalssiffran 7 har värdet 70 och entalssiffran 2 har värdet 2.
Talet 72 skrivet i utvecklad form blir därför
70+2 - Talet 137 består av siffrorna 1, 3 och 7, där hundratalssiffran 1 har värdet 100, tiotalssiffran 3 har värdet 30 och entalssiffran 7 har värdet 7.
Talet 137 skrivet i utvecklad form blir därför
100+30+7 - Talet 720 består av siffrorna 7, 2 och 0, där hundratalssiffran 7 har värdet 700, tiotalssiffran 2 har värdet 20 och entalssiffran 0 har värdet 0.
Vi behöver inte ta med siffror som har värdet 0 när vi skriver ett tal i utvecklad form. Därför blir talet 720 skrivet i utvecklad form
700+20
Udda och jämna tal
| Känner du till indelningen udda och jämna tal? Talen 0, 2, 4, 6, 8 kallas jämna siffror eller tal. Talen 1, 3, 5, 7, 9 kallas udda siffror eller tal. Det medför då att: |
|
Udda och jämna tal - Udda och jämna tal
Tal och siffror
I vårt tiotalsystem använder vi oss av tio siffror för att bygga upp alla tal. Siffrorna vi använder oss av är naturligtvis:
Ett exempel på ett tal är 157 som byggs upp av siffrorna 1, 5, och 7.
Talet 1 308 byggs upp av siffrorna 1, 3, 0 och 8.
Ett exempel på ett tal är 157 som byggs upp av siffrorna 1, 5, och 7.
Talet 1 308 byggs upp av siffrorna 1, 3, 0 och 8.
Hitta rätt antal objekt
Tid (Enheter och begrepp)
Det finns många måttenheter för tid. En del är vanligare än andra.
Sekund
Förkortas s. Sekund är standardenheten (SI-enheten) för tid.
Hur långt är egentligen en sekund? Vad hinner du göra på en sekund? På 10 sekunder?
Minut
Förkortas min. 1 minut = 60 sekunder.
Kvart
En kvart = 15 minuter.
Vad hinner du att göra på en kvart?
Timme
Inom matematiken och fysiken förkortas timme ofta med h, från engelskans hour.
1 timme = 60 minuter = 3 600 sekunder.
Dag
Dagen är den ljusa delen av dygnet det vill säga tiden mellan solens upp- och nedgång, motsatsen till natt. Dagarnas längd varierar beroende på årstider och var på jordklotet du befinner dig.
Dygn
24timmar. Den tid det tar för jorden att rotera ett varv runt sin egen axel.
Vecka
7 dagar. Starten för en ny vecka är måndag och den avslutas därav med söndag. Vi har 52 hela veckor på ett år.
Månad
Antalet dagar i en månad varierar mellan 28 – 31 beroende på månad.
Vart fjärde år är det skottår och då har Februari 29 dagar istället för 28. Det går fyra veckor på en månad.
År
Den tid det tar för jorden att fullborda ett varv runt solen. 365 dagar
Årtionde - decennium
En period som omfattar 10 år. T ex 1954 – 1964. Ofta menar man jämna 10-tals år. Exempelvis 1980-1989 eller 1990-1999.
Århundrade – sekel
En period som omfattar 100 år. T ex 1880 – 1980. Ofta menar man jämna 100-tals år. Exempelvis 1700-talet (år 1700 – år 1799).
Årtusende – millennium
En period som omfattar 1 000 år. T ex 560 -1560. Ofta menar man jämna 1000-tals år. Exempelvis 1000-talet (år 1000-1999) och 2000-talet
(år 2000 – 2999). Vi lever nu på 2000-talet.
 |
Du kan använda knogarna för att komma ihåg hur många dagar varje månad har.
Håll upp händerna bredvid varandra. Börja från vänster, med januari. Varje knoge motsvarar 31 dagar och mellan två knogar motsvarar 30 dagar. Undantaget är februari som ju har 28 eller 29 dagar. |
Kvartal
Året är indelat i 4 kvartal, d v s varje kvartal består av 3 månader.
| 1:a kvartalet: Januari, Februari och Mars 2:a kvartalet: April, Maj och Juni 3:e kvartalet: Juli, Augusti och September 4:e kvartalet: Oktober, November och December |
 |
Årstid
|
I Sverige har vi fyra årstider; vår, sommar, höst och vinter. En förenklad bild av hur årstiderna fördelar sig under året ser du här till höger. |
 |
Enhetsomvandling Lösningar
| Enhetsomvandling | ||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
4. Hur många hela och hur många delar visar dessa bilder?
| 4. Hur många hela och hur många delar visar dessa bilder? | |||
|
|||
3. Storleksordna bråken. Börja med det minsta
| 3. Storleksordna bråken. Börja med det minsta. | |||
|
|||
2. Ange om bråket är mindre än, större än eller lika med 1.
| 2. Ange om bråket är mindre än, större än eller lika med 1. | |||
|
|||
1. Vilket av de två bråken är störst? Svar
| 1. Vilket av de två bråken är störst? | |||
|
|||
Rätt svar
 |
 |
 |
| a) | b) | c) |
| åttondelar | ||
 |
 |
 |
| d) | e) | f) |
| åttondelar | åttondelar |
Rätt svar
 |
 |
 |
| a) | b) | c) |
| fjärdedelar | fjärdedelar | |
 |
 |
 |
| d) | e) | f) |
| fjärdedelar |
Mjölkens väg
Klicka på bilden för att titta på filmen
Kan du svara på de här ko-frågorna nedan. Skriv svaren i kommentarerna
(Du får svaren om du tittar på filmen)
1. Hur många kilo gräs kan en ko äta per dag?
1. 10 kg
x. 5 kg
2. 70 kg
2. Hur mycket mjölk ger en ko per dag ungefär?
1. 5 liter
x. 10 liter
2. 30 liter
3. Hur många gånger per dag mjölkas en ko?
1. 1 gång
x. 2 gånger
2. 4 gånger
4. Hur många magar har en ko?
1. 1
x. 2
2. 4
5. Hur mycket vatten kan en ko dricka per dag?
1. 20 liter
x. 100 liter
2. 1000 liter
Decimaltal
Decimaltal
| Sträckan i linje mellan 0 och 1 är uppdelad i tio delar. Var och en av dessa tio delar är En tiondel |
Räkna
|
|
|
||||||||||||||||||||||||||||||||
Taluppfattning
|
Matematik övningar
Vad är litteracitet på hög nivå?
Litteracitet innefattar mycket mer än läsförståelse och avkodning.
Olika ämnen kräver olika litterata förmågor.
Att vara litterat inom ett ämne innebär att man förstår hur de grundläggande principerna i ämnet är organiserade och värderade.
Generellt tenderar skolspråk att vara mer "som skriftspråk", mindre personligt, mer abstrakt, mer explicit, ha större lexikalisk täthet och vara mer strukturerat än elevernas vardagsrelaterade språk.
Exempel på en uppgift…
Utforma en uppgift till dina elever som bygger på de flesta av följande kriterier:
•Det finns ett verkligt behov av att tala.
•Språket används i ett autentiskt syfte
•Uppgiften är en del av kursmomentet
•Uppgiften är intressant och relevant för elevernas studier
•Uppgiften är kognitivt utmanande på en nivå som är lämplig för den årskurs eleverna
går i.
•Uppgiften kräver att alla deltar
•Uppgiften kräver att eleverna verkligen utnyttjar språket till fullo
•Det bör finnas ett ”informationsgap” eftersom eleverna sitter inne med olika
information eller åsikter
•Uppgiften ska ha ett tydligt mål,t ex att man löser ett problem eller utbyter
information. (P.Gibbons 2010)
Litteraciteten under den senare delen av grundskolan
- Vid övergången till åk 4 tenderar antalet litteracitetsbaserade uppgifter och användningen av ämnesrealterat skolspråk att öka
- Från åk 7 blir den ämnesspecifika språkfärdigheten och skolspråket allt viktigare för kunskapsinhämtandet.
- När eleverna går från högstadiet till gymnasiet måste de behärska ämnesrelaterat språk på hög nivå och en ständigt ökande mängd abstrakta begrepp
Lyft tänkandet - språk och lärande i ett andraspråksperspektiv
Engagemnag för och utveckling av litteracitet i en kognitivit krävande undervisning.
Arbeta undersökande och bygga upp kunskap genom utvecklande samtal.
Kognitivt krävande uppgifter och mycket stöttning (dels genom planering, dels genom interaktion i klassrummet) är extra viktigt för eleverna.
Lärare ifrågasätter sina egna förväntningar på elevernas kapacitet.
Ett samband mellan höga förväntningar från läraren och bättre elevprestationer.
Aritmetik
Definition: gren av matematiken där man studerar addition, subtraktion, multiplikation, division, potenser och rotutdragning av tal.
Historia: Aritmetiken har sina rötter i de antika civilisationerna. I Europa var senare aritmetik en av de sju fria konsterna i den medeltida undervisningen; den ingick i den första gruppen, quadrivium, tillsammans med geometri, musik och astronomi. De tre övriga ingick i den andra gruppen, trivium, som bestod av grammatik, retorik och dialektik.
Etymologi: Aritmetik kommer från grekiskans arithm¯etik¯e´ ’räknekonst’, avlett av arithmós ’tal, antal’.
FBG Matematik
Eleverna jobbar med både matematiska ord och matematiska terminologi:
t.ex: Öka - Addera
Minska - Subtrahera
Dubbla eller dubbelt - Multiplicera
Halvera eller hälften - Dividera
Eleven utvecklar sin förmåga att använda matematikens uttrycksformer för att samtala om, argumentera och redogöra för frågeställningar, beräkningar och slutsatser (Skolverket, 2011, s. 63).
Att förstå ord och begrepp skulle vara mycket givande både för barnens språkutveckling och för matematikinlärning (Elbers & de Haan, 2005).
Det är viktigt att vi tillåter nyanlända elever att uttrycka sig på matematiklektionen på sitt modersmål.
Lässtrategiers betydelse för elever med svenska som andraspråk
Goda lässtrategier kan kompensera de problem som brister i ordförståelse och förkunskaper orsakar.
(Andreassen, 2008, Liberg, 2010, Stensson, 2006, Westlund, 2009).
Andraspråkselever löper större risk att vara mindre bekanta med textens innehåll, ämnesområde och språk och behöver därför lära sig lässtrategier, dels för att förstå texten de läser och dels för att lära sig strategier att hantera nya texter i andra sammanhang
(Gibbons, 2010)
Läsförståelse på ett andraspråk
Andraspråksinlärare löper ökad risk att flera av faktorerna hos läsaren brister, däribland förkunskaper och ordförråd (Viberg (1993)
Ordförrådet är den enskilt viktigaste språkliga faktorn för tillägnandet av kunskaper i skolans ämnesundervisning (Viberg,1993).
Det betyder att läsare på ett andraspråk redan i det första läget, när det gäller att avkoda det som står på raderna, kan stöta på problem vid läsningen.